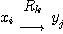Jak bylo uvedeno v předcházející kapitole, rozvoj problematiky řešení úloh byl v počátečních fázích inspirován poměrně naivní představou, že by výpočetní systém mohl samostatně řešit úlohy, u nichž nalezení uspokojivého řešení člověku činí jisté obtíže. Druhou představou je přenesení rutinních činností souvisejících s řešením např. skupiny podobných či příbuzných úloh na výpočetní systém. Tato představa je pro odborníka z oblasti výpočetní techniky již poněkud přijatelnější, neboť odpovídá smyslu využívání výpočetní techniky. V praxi pak obvykle jde o nalezení některého konkrétního, z některého hlediska optimálního (častěji přibližně optimálního) postupu řešení, přičemž zadavatel musí být schopen úlohu formálně správně a hlavně jednoznačně formulovat. Do oblasti řešení úloh patří také problematika hraní her, neboť ve svém principu i zde zpravidla jde o nalezení nejsnazší cesty jak dosáhnout kýženého cíle - vyhrát nad soupeřem.

Stručně jsme uvedli, že každá úloha musí být formálně definována (popsána) výchozím stavem, množinou cílových stavů (která může obsahovat pouze jediný prvek nebo cílový stav nemusí být předem explicitně zadán a je dán obecně platnými podmínkami - viz šachové úlohy) a množinou přípustných akcí, resp. operací. úkolem výpočetního systému vybaveného umělou inteligencí pak je nalezení takové posloupnosti přípustných akcí (operací), která úlohu převede ze zadaného výchozího stavu do některého stavu cílového. Prvním naším úkolem proto bude zavedení takového formálního aparátu, který nám umožní každou úlohu jednoduše, přehledně a přitom jednoznačně definovat.

2.1 Úloha a teorie řešení úloh

U každé úlohy nejprve uvažujme dvě množiny stavů (jevů, pozorování, tvrzení,...) X = {x₁,x₂,...} Y = {y₁,y₂,...}, které nazveme množinou vstupních, resp. výstupních stavů, a o nichž předpokládáme, že mezi nimi existuje vztah modelovaný operátorem R_k z množiny R takový, že

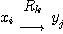,                 i,j,k = 1, 2, ..

Množiny X,Y mohou být konečné i nekonečné. Popsanou situaci lze jednoduše zapsat trojicí (X,Y,R).

Úlohou nazveme situaci, kdy známe dvě složky z trojice (X,Y,R) a hledáme zbývající složku. Proces hledání zbývající (chybějící) složky pak nazveme hledáním řešení úlohy. Teorie řešení úloh (Problem Solving Theory) se zabývá zkoumáním obecných metod, jak řešit libovolnou úlohu, tj. jak nalézt chybějící složku v trojici (X,Y,R). Teorii řešení úloh tedy nezajímá řešení jedné konkrétní úlohy, nýbrž nalezení obecné metody, jak postupovat při hledání řešení rozmanitých úloh z nějaké dostatečně bohaté množiny úloh.

Podle toho, která složka z (X,Y,R) není známa, rozlišujeme tři typy úloh:

1. úlohy deduktivní - u nichž hledáme množinu výstupních stavů (de facto množinu možných řešení úlohy); situaci můžeme symbolicky vyjádřit jako trojici (X,?,R),
2. úlohy abduktivní - u nichž známe množinu výstupních stavů a množinu přípustných akcí (operací) a hledáme množinu vstupních stavů - (?,Y,R),
3. úlohy induktivní - u nichž jsou známy množiny X a Y a hledáme množinu akcí, která převádí úlohu z některého z výstupních stavů do některého z výstupních (X,Y,?).

Dedukce je zcela mechanický proces produkující vždy jen jedinou množinu řešení, která nazýváme řešeními exaktními. Výsledkem abdukce může být exaktní řešení, pokud zobrazení definované operátorem R_k, R_k je z množiny R, k=1,2,... je bijektivní (tj.prosté a na). V opačném případě můžeme mechanicky určit (aplikací inverzních operátorů R_k^-1,R_k z R, k=1,2...) možné výsledky. Žádný z těchto výsledků však není exaktní; každý z nich je pouze hypotézou, neboť ze zadání úlohy nelze rozhodnout, který z výsledků je "ten pravý". U indukce je situace ještě obtížnější. Řešení, tj. nalezený operátor, resp. posloupnost operátorů, je vždy hypotézou. Avšak na rozdíl od abdukce je informace obsažená v zadání úlohy natolik malá, že možné operátory neumíme ze samotného zadání algoritmicky odvodit. Formulace hypotéz u induktivních úloh je v pravém slova smyslu tvořivá činnost, k níž člověk využívá analogií, vizuálních představ aj. Přesto si není získaným výsledkem jist a zformulovanou hypotézu musí zpětně deduktivně prověřovat, zda vyhovuje zadaným množinám stavů X a Y.

Výše uvedené skutečnosti lze ilustrovat pomocí následujícího příkladu:

Příklad 2.1:  Nechť X = {2} Y = {2} a R a obsahuje jedinou operaci, a to umocnění dvěma. Potom:

• Dedukce: dáno X={2}, R{x²}; výsledkem je Y={4};
• Abdukce: dáno Y={4}, R{x²}; výsledkem je X={-2,2};
• Indukce: X={2}, Y={4}; R obsahuje zřejmě umocnění dvěma, ale také by mohla obsahovat násobení dvěma a přičtení dvou.

Jako další praktické příklady lze uvést:

• Dedukce: Výpočet odezvy dynamického systému na zadaný vstupní signál, běh programu na číslicovém počítači;
• Abdukce: Lékařská a technická diagnostika, použití znalostních a expertních (konsultačních) systémů;
• Indukce: Identifikace systému, hledání důkazu matematické věty, formulování zákonitostí v přírodních a společenských vědách, sestavení programu pro počítač nebo plánu činnosti robota či syntéza regulátoru ze zadaných vstupních a výstupních specifikací.

Nás bude v dalším zajímat především řešení induktivních úloh, protože deduktivní nebo abduktivní úlohy jsou díky své mechaničnosti v podstatě jednoduché. Analogii a vizuální představivost ale dosud neumíme naprogramovat, a tak při formulování hypotéz postupujeme dvěma způsoby:

1. Apriorně zvolíme množinu operátorů, kterou zpravidla parametrizujeme, a nastavováním vhodného parametru vybíráme takový operátor, který vyhovuje zadaným množinám stavů X a Y. Takový přístup je využíván např. v teorii řízení, u učících se systémů aj.
2. Apriorně zvolíme konečnou množinu elementárních operátorů, ze kterých se snažíme skládáním vytvořit výsledný, tzv. kompoziční operátor, který vyhovuje zadaným množinám X a Y. Tento způsob je základem všech dosavadních postupů hledání řešení úloh, které byly v oblasti umělé inteligence zatím vytvořeny.

Oba uvedené způsoby obecně dovolují vybírat vhodnou hypotézu R z nekonečně mnoha variant, přičemž - jak už bylo řečeno výše - postup výběru hypotézy obecně nevyplývá ze zadání úlohy. V tomto smyslu jsou induktivní úlohy nedeterministické. Nedeterminismus je jedním z klíčových pojmů umělé inteligence, a proto mu věnujme samostatný odstavec.

Hlavolam "8" má na desce o 3 x 3 políčkách osm průběžně očíslovaných kamenů, deváté políčko je volné. Přesouváním kamenů na volné políčko je možné postupně měnit uspořádání kamenů. úkolem člověka (nebo "inteligentního" stroje) bude ze zadaného výchozího (počátečního) uspořádání kamenů dosáhnout jejich postupným přesouváním zadaného cílového uspořádání, např.:

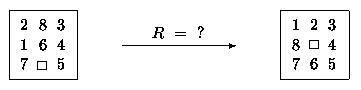
Zřejmě jde o induktivní úlohu: výchozí (počáteční) uspořádání (stav) a cílové uspořádání jsou jednoprvkové množiny X, resp. Y, množina elementárních operátorů je dána pravidly hry, která bychom si mohli představit např. jako posuvy prázdného políčka (v obrázku prázdný čtverec) nahoru, dolů, doleva, doprava, přičemž prázdné políčko samozřejmě nesmí opustit hrací desku. Pravidla hry můžeme obecně zapsat jako

if  podmínka then akce,

což v dalším budeme stručněji zapisovat ve tvaru podmínka akce. Jednotlivá pravidla pro přesouvání kamenů (operátory) pak budou mít následující podobu (prázdné políčko nazvěme "blank"):

 

"blank" není v horním řádku    posuň "blank" nahoru,

"blank" není v dolním řádku    posuň "blank" dolů,

"blank" není v levém sloupci    posuň "blank" doleva

"blank" není v pravém sloupci    posuň "blank" doprava .

Pravidla hry spolu se zadáním výchozího a cílového uspořádání kamenů představují vše, co dokážeme z formulace úlohy získat. Je to informace značně neúplná, neboť na každý stav můžeme aplikovat vždy nejméně dvě pravidla a ze zadání úlohy nevyplývá, které z nich máme vybrat. Právě v tom spočívá nedeterminismus této úlohy. Nemáme-li žádnou informaci o tom, které z pravidel aplikovatelných na daný stav vybrat, musíme vybírat náhodně s rizikem, že náš výběr bude chybný. Pokud později chybu objevíme, musíme se vrátit až do místa vzniku chyby. Z toho důvodu si musíme místa, ve kterých přijímáme náhodná rozhodnutí, pamatovat a říkáme jim uzly větvení. Proces hledání řešení úlohy je pak metodou pokusů a omylů (někdy též říkáme metodou zkoušek a chyb). Proces hledání řešení úlohy můžeme znázornit acyklickým grafem, který budeme dále nazývat stromem řešení úlohy (strom řešení výše uvedené úlohy "hlavolam 8" je znázorněn na obr. 2.1). Uzly stromu jsou uzly větvení, hrany stromu představují jednotlivé alternativy postupu řešení (aplikace pravidel pro přesouvání kamenů), které jsme již vyzkoušeli.

Důsledkem nedeterminismu v řešení úloh je, že nalezení správného řešení úlohy může trvat velmi dlouho nebo proces hledání řešení dokonce neskončí vůbec. Proto se obvykle snažíme získat nějakou další doplňující informaci o úloze, na jejímž základě bychom mohli zformulovat kritérium umožňující vybírat jen takové hypotézy, které mají největší naději vyhovět daným množinám stavů, a ty potom deduktivně prověřovat. Této doplňující informaci říkáme heuristika, protože pomáhá nalézt řešení (heuréka = už jsem na to přišel!). Na rozdíl od exaktních poznatků u heuristik přesně nevíme, za jakých předpokladů jsou pravdivé. Víme jen, že jsou pravdivé v běžných, typických situacích.

Přidáním heuristiky přestává být úloha čistě induktivní, neboť kromě množin stavů X a Y známe apriorně něco i o operátorech. R_k z množiny R. Tím více či méně omezíme nedeterminismus úlohy a hledání řešení se zjednoduší, i když v jednotlivých případech nalezení řešení nemusí být kratší (rychlejší).

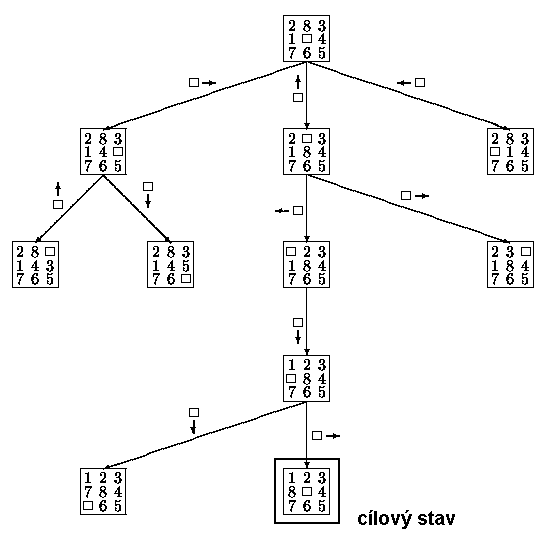
Obr.2.1: Strom řešení úlohy hlavolam "8"

Aby bylo možno nalezení řešení dané úlohy "svěřit počítači", je při dnešních možnostech výpočetních systémů zcela nezbytné řešenou úlohu jednoznačně popsat, tj. vytvořit tzv. formální popis úlohy. Jak již bylo naznačeno výše, úlohu míváme obvykle definovánu počátečním, resp. výchozím stavem, množinou konečných, resp. cílových stavů a množinou pravidel, která nám umožňují převést úlohu postupně (v jednotlivých krocích) ze stavu výchozího do stavu cílového. Během postupu řešení úlohy, tj. při aplikaci jednotlivých pravidel, hovoříme o přechodech úlohy z jednoho stavu do stavu dalšího, přičemž všechny stavy, které jsme prošli na cestě ze stavu výchozího do některého stavu cílového, nazveme mezilehlými nebo též vnitřními stavy úlohy. úloha je pak jednoznačně popsána množinou stavů, v nichž se může nacházet (a z nichž některé můžeme definovat jako stavy výchozí a jiné jako stavy cílové), a množinou pravidel pro přechody mezi stavy. Takový popis úlohy nazveme popisem stavovým, resp. reprezentací úlohy ve stavovém prostoru. Množinu stavů, v nichž se může úloha nacházet, nazveme stavovým prostorem úlohy.

Z hlediska realizace postupu hledání řešení úlohy na počítači obvykle hovoříme o popisu stavů obsahem databáze, cílový stav podmínkou, kterou musí obsah databáze splňovat, a přechody mezi stavy pravidly, jak databázi, resp. její obsah měnit. Tato pravidla jsou de facto zobecněnou formou přepisovacích pravidel známých z teorie formálních jazyků a nazývají se produkční pravidla.

Reprezentace úlohy ve stavovém prostoru závisí na celé řadě faktorů. Jsou jimi zejména typ úlohy, produkční pravidla, možnosti zvoleného programovacího jazyka či programového systému apod. Při volbě reprezentace bude zřejmě dominantním požadavkem požadavek co nejúčinnější a nejpohodlnější manipulace s úlohou. Je možné volit např. řetězce symbolů, vektorovou reprezentaci, maticovou reprezentaci, stromové nebo seznamové struktury. Produkční pravidla jsou realizována operátory. Operátory provádějí transformaci jednoho stavu úlohy na jiný stav. Lze je chápat jako zobrazení jednoho prvku stavového prostoru do jiného prvku tohoto prostoru. Protože při řešení úloh pracujeme s popisy stavů, lze předpokládat, že operátory jsou funkcemi těchto popisů stavů a funkční hodnoty jsou vždy popisy stavu. Teoreticky by bylo možné tuto funkci reprezentovat tabulkou, která každému "vstupnímu" stavu přiřadí jistý stav "výstupní". Prakticky to však nebývá možné, neboť počet stavů konkrétní úlohy bývá příliš vysoký a tabulku by se nám nepodařilo umístit do paměti, nehledě k tomu, že vytvoření takové tabulky není triviální záležitostí.

Hledání řešení úlohy pomocí její reprezentace ve stavovém prostoru nazveme hledáním ve stavovém prostoru. Prohledávání stavového prostoru lze poměrně jednoduše popsat grafem. Jednotlivé stavy úlohy odpovídají uzlům grafu, přechody mezi stavy hranám. Jednomu z uzlů odpovídá počáteční stav úlohy, následující uzly představují stavy mezilehlé (nebo vnitřní), do nichž lze z počátečního stavu přejít atd. Hrany grafu obvykle orientujeme, čímž vyznačujeme směry prohledávání stavového prostoru. Uzel grafu n_j, do něhož z uzlu n_i vede orientovaná hrana, nazveme bezprostředním následníkem uzlu n_i. Naopak uzel n_i nazýváme bezprostředním předchůdcem uzlu n_j. Nalezení všech bezprostředních následníků uzlu n_i označujeme jako expanzi tohoto uzlu. Počet orientovaných hran od výchozího uzlu grafu do daného uzlu označujeme jako hloubku uzlu. Máme-li např. úlohu reprezentovánu stromovým grafem uvedeným na obr.2.1, pak výchozí stav úlohy leží v kořeni stromu a má hloubku 0, uzel grafu reprezentující cílový stav řešení úlohy je listem a má hloubku 4.

Každý přechod mezi dvěma stavy můžeme ohodnotit kladným číslem. Toto číslo lze chápat jako cenu, resp. náklady, které musíme vynaložit na přechod (použití produkčního pravidla) ze stavu n_i do stavu n_j. V grafové reprezentaci je přiřazena cena jednotlivým hranám. Pokud existuje posloupnost orientovaných hran (cesta) z uzlu n_i do uzlu n_k, ohodnotíme přechod z uzlu n_i do uzlu n_k součtem cen (nákladů) příslušných hran. Často nás zajímá nalezení nejmenší ceny cesty (nejmenších nákladů) z výchozího uzlu do uzlu n_k.

V předchozím odstavci jsme na příkladu hlavolamu "8" naznačili, že zdánlivě i značně různorodé induktivní úlohy a postup jejich řešení lze popsat jednotným způsobem, pomocí speciálního formalismu. Tento formalismus se nazývá produkční systém. Produkční systém je odvozen z Postových systémů a Markovových algoritmů, což jsou systémy za určitých podmínek ekvivalentní Turingovým strojům.

Produkční systém sestává z následujících částí:

1. Databáze úlohy obsahuje fakta, což jsou specifické poznatky (údaje) týkající se právě (pouze jen) řešené úlohy. Z hlediska způsobu reprezentace jsou fakta uložená v databázi úlohy reprezentována zpravidla deklarativně.
2. Báze znalostí obsahuje produkční pravidla, což jsou obecné poznatky, resp. postupy použitelné v právě řešené úloze, ale také pro řešení celé třídy podobných úloh (někdy říkáme úloh stejného nebo podobného charakteru). Produkční pravidla si můžeme představit jako procedury, které daným způsobem mění obsah databáze. Každé produkční pravidlo má tvar

   podmínka      akce

   Jestliže některá data uložená v databázi splňují podmínku uvedenou na levé straně produkčního pravidla, může být produkční pravidlo provedeno (provedena předepsaná akce). Z implementačního hlediska se vlastně jedná o podmíněné volání procedury nebo funkce, která danou akci realizuje. Z hlediska způsobu reprezentace znalostí se zde jedná o procedurální reprezentaci.

3. Řídicí mechanismus nezávisí na řešené úloze. Jeho úkolem je:
   • provést volbu, které aplikovatelné pravidlo bude v daném okamžiku použito,
   • vybrat fakta z databáze, která budou dosazena do podmínky zvoleného produkčního pravidla,
   • ukončit řešení (výpočet), je-li splněna cílová podmínka.
4. Množina cílů, které mají být splněny.

Cílová podmínka, při jejímž splnění řídicí mechanismus ukončuje řešení (výpočet), může být dvojího druhu:

1. explicitní, odvozená z množiny cílů,
2. implicitní, nejde-li na daný obsah databáze aplikovat žádné další produkční pravidlo.

Řídicí mechanismus je nejdůležitější částí produkčního systému, neboť především na něm záleží, po kolika krocích (či zda vůbec) bude dosaženo cílové podmínky a tak nalezeno hledané řešení. Řídicí mechanismus může pracovat ve dvou režimech:

1. Přímochodý (forward) režim se vyznačuje tím, že při použití produkčního pravidla se nejprve prověřuje podmínka a je-li tato splněna, provede se akce (z implementačního pohledu se vyvolá příslušná procedura). Tento postup se opakuje do té doby, až aktuální obsah databáze splňuje cílovou podmínku. Řízení tedy postupuje od počátečního obsahu databáze odpovídajícího počátečnímu stavu v řešení úlohy směrem k takovému obsahu databáze, který odpovídá některému z cílových stavů úlohy.
2. Zpětnochodý (backward) režim se vyznačuje tím, že při použití pravidla se nejprve prověřuje jeho akce a je-li jejím výsledkem obsah databáze odpovídající cíli řešení, snaží se naplnit podmínky tohoto pravidla. Tento postup opakuje tak dlouho, až se podaří nalézt takový obsah databáze, který odpovídá výchozímu stavu úlohy.

V odstavci 2.3 jsme řekli, že:

• stav úlohy je představován uzlem (vrcholem) stromového grafu,
• počátečnímu stavu úlohy odpovídá kořen stromového grafu,
• některé z koncových uzlů (vrcholů) grafu odpovídají cílovým stavům,
• orientovaná hrana vedoucí z uzlu n_i do uzlu n_j reprezentuje přechod z i-tého stavu do stavu nového (j-tého),
• aplikací všech produkčních pravidel (operátorů) na daný stav úlohy dostaneme všechny možné následující stavy úlohy (provedeme expanzi uzlu).

Hledání řešení úlohy spočívá v nalezení cesty, která spojuje počáteční uzel grafu s uzlem koncovým, který představuje cílový stav (cíl řešení úlohy). Při hledání cesty v grafu můžeme postupovat jak ve smyslu orientace hran, tj. od uzlu počátečního k uzlu koncovému (cílovému) - pak hovoříme o režimu prohledávání grafu přímém, resp. přímochodém, tak obráceně, tj. proti smyslu orientace hran - potom hovoříme o režimu prohledávání zpětném, resp. zpětnochodém, což je v souladu s tvrzeními uvedenými v předcházejícím odstavci.

Řídicí strategie generuje strom řešení, který je podgrafem orientovaného grafu reprezentujícího stavový prostor. K tomu, aby bylo dosaženo řešení (hledané řešení bylo nalezeno), je třeba se umět v grafu "pohybovat", což zajišťuje právě výše zmíněná řídicí strategie. Cílem řídicích strategií je efektivní prohledávání poměrně rozsáhlých stavových prostorů řešených úloh. Efektivnost spočívá buď ve výběru nejvhodnějšího produkčního pravidla (operátoru), jehož aplikací se nový stav přiblíží k cílovému stavu, nebo ve výběru vhodného vrcholu k expanzi. Řešitel se proto snaží získat ze zadání úlohy informace, které by úlohu více specifikovaly a tím omezily kombinatorickou expanzi stavů úlohy. Tyto informace se označují jako heuristické, neboť jejich exaktnost nelze prokázat.

Z popisu řídicího mechanismu, který realizuje zvolenou řídicí strategii, vidíme, že obsahuje nedeterminismus: blíže neurčený pokyn "vyber". Přitom tušíme, že právě výběr produkčních pravidel a faktů z databáze má rozhodující vliv na postup řešení úlohy. Řídicí mechanismus si kromě toho musí "pamatovat" již vyzkoušené posloupnosti použitých pravidel a vygenerovaných obsahů databází (vygenerovanou část stromu řešení). Většinou ale má řídicí mechanismus k dispozici pouze neúplnou informaci pro výběr nejvhodnějšího pravidla, a proto musí obsahovat také postupy hledání, při kterém zkouší různé posloupnopsti pravidel, dokud nenajde takové řešení, jehož obsah databáze vyhovuje cílové podmínce.

Řídicí strategie rozdělujeme podle způsobu aplikace pravidel (operátorů) na dvě skupiny:

1. neodvolatelné (irrevocable) - tj. takové, které aplikují pravidlo (operátor) tak, že tento výběr operátoru už nelze později změnit,
2. pokusné (tentative) - tj. takové, které umožňují v případě potřeby vrátit se k určitému uzlu a na stav odpovídající uzlu, do něhož jsme se vrátili, aplikovat jiné pravidlo (operátor).

Při neodvolatelné řídicí strategii je vybráno nějaké aplikovatelné produkční pravidlo a je nenávratně aplikováno na daný obsah databáze bez možnosti tento výběr později změnit (vrátit). Tato strategie je použitelná jen pro nejjednodušší úlohy (doslova jen hříčky), jakou je např. již zmíněný hlavolam "8". Aby neodvolatelná řídicí strategie nebyla naprosto neinformovaná, může vybírat produkční pravidlo podle nějakého dodatečného předpisu. Pro hlavolam "8" zvolíme např. gradientní metodu. K tomu definujeme vhodnou "ohodnocující" funkci, která pro libovolný obsah databáze vypočte jeho ohodnocení. Řídicí mechanismus pak vybírá takové produkční pravidlo, které produkuje obsah databáze s největším přírůstkem, resp. úbytkem ohodnocení. Jestliže takové pravidlo neexistuje, vybere se alespoň takové pravidlo, které ohodnocení nezmění. Jestliže ani taková možnost neexistuje, řešení úlohy (výpočet) se obvykle zastaví a signalizuje neúspěch v hledání řešení. Bližším rozborem se dá usoudit, že gradientní metody jsou ve svých možnostech také velmi omezené a k cíli vedou opět jen u těch nejjednodušších úloh.

Příklad 2.2:  U hlavolamu "8" můžeme za ohodnocení vzít záporně vzatý počet kamenů, které nejsou na svém místě. Příklad použití neodvolatelné strategie pro řešení "8" je uveden na obr. 2.2.

Obr.2.2:  Řešení hlavolamu "8" při použití gradientní metody

Při pokusné řídicí strategii se používá hledání řešení spojené s konstrukcí stromu řešení. Uzly stromu řešení odpovídají jednotlivým stavům řešení úlohy reprezentovaným příslušnými obsahy databáze, hrany pak použitým produkčním pravidlům. Jestliže řídicí mechanismus vybere nějaké aplikovatelné produkční pravidlo, zapamatuje si původní obsah databáze i použité produkční pravidlo (tj. "rozšíří" strom řešení) a teprve potom toto produkční pravidlo aplikuje na aktuální obsah databáze. Díky tomu se řídicí mechanismus může v případě potřeby vrátit k předchozímu uzlu stromu řešení (předchozímu obsahu databáze) a na původní obsah databáze použít jiné aplikovatelné pravidlo.

Pokusné strategie se při hledání řešení úloh využívají poměrně hodně a dále se člení na strategie slepé a cílené (viz dále).

2.5.1 Mechanismus navracení (backtracking)

Činnost mechanismu navracení (backtracking) můžeme ve stručnosti popsat zhruba takto:
Při výběru produkčního pravidla aplikovatelného na daný obsah databáze vytvoří řídicí mechanismus uzel větvení a zapamatuje si původní obsah databáze a aplikované pravidlo. Potom toto pravidlo aplikuje a vytvoří nový obsah databáze. Jestliže se při hledání řešení dostane do stavu, který označíme jako chybový (fail) - viz dále, vrátí se řídicí mechanismus k poslednímu vygenerovanému uzlu větvení, resp. k jeho databázi, a vybere v pořadí další aplikovatelné pravidlo. Jestliže takové pravidlo již neexistuje, zruší tento uzel větvení a přejde na bezprostředně předcházející uzel větvení.

Chybový stav (fail), tj. pokyn k návratu, může nastat v těchto případech:

1. nově vygenerovaný uzel se již v zapamatované cestě stromu řešení vyskytuje (tj. došlo by k "zacyklení" algoritmu),
2. bylo dosaženo zadané maximální hloubky stromu řešení, aniž by bylo řešení úlohy (cílový stav) nalezeno,
3. ze zadání úlohy explicitně plyne, že právě vygenerovaný uzel určitě neleží na cestě vedoucí k řešení úlohy.

Z popsané činnosti mechanismu je zjevné, že produkční pravidla musejí být nějakým způsobem seřazena, aby se řídicí mechanismus mohl orientovat, která pravidla již byla použita (vyzkoušena) a které pravidlo má být vybráno jako další. Mechanismus navracení si obvykle pamatuje pořadové číslo použitého pravidla.

Z uvedeného popisu činnosti mechanismu navracení vyplývá, že mechanismus si pamatuje vždy jen jedinou cestu stromu řešení vedoucí od kořene k poslednímu vygenerovanému uzlu. Proto je mechanismus navracení snadno implementovatelný a někdy se mu proto dává přednost před dokonalejšími řídicími strategiemi. Jeho nevýhodou je skutečnost, že musí znovu procházet a rozvíjet uzly (stavy), ve kterých již dříve byl a které "zapomněl". Jako vždy i zde stojí proti sobě dva faktory algoritmické složitosti: čas a paměť. Backtracking dává přednost malé potřebě paměti za cenu vyšších nároků na čas potřebný k výpočtu.

Mechanismus navracení se obvykle implementuje tak, že cesta, kterou si má řídicí mechanismus zapamatovat, se reprezentuje jako zřetězený seznam nebo zásobník, jehož prvky jsou tvořeny dvojicemi (databáze, použité pravidlo), přičemž poslední vygenerovaná dvojice se vždy ukládá na začátek seznamu, resp. na vrchol zásobníku. Dostane-li se mechanismus do tzv. chybového (fail) stavu, vezme se databáze z první dvojice uchované v seznamu (zásobníku) a použije se další pravidlo; mechanismus navracení však v tomto případě musí změnit použité pravidlo v první uchované dvojici. Jestliže žádné další produkční pravidlo již neexistuje, zruší se první dvojice v seznamu (na vrcholu zásobníku), vezme se databáze z dvojice, která byla původně na druhém místě, a aplikuje se další v pořadí příslušné pravidlo.

Popsaný algoritmus lze schématicky zapsat následovně [Nilsson82]

Recursive procedure BACKTRACK ( DATA)

1. if TERM ( DATA) then return NIL; {TERM; je logická funkce (predikát) nabývající hodnoty true v případě, že obsah databáze DATA splňuje cílovou podmínku implementovaného produkčního systému. Jako příznak úspěšného ukončení hledání řešení je procedurou vracen NIL, resp. prázdný seznam.}
2. if DEADEND ( DATA) then return FAIL; {DEADEND je logická funkce nabývající hodnoty true v případě, že mechanismus se dostal do chybového (fail) stavu (podmínky viz výše) a nelze dále úspěšně pokračovat vpřed k hledanému cíli řešení. V takovém případě vrací procedura symbol FAIL jako příznak dosažení chybového stavu.}
3. RULES APPRULES ( DATA); { APPRULES je funkce určující, která produkční pravidla a v jakém pořadí budou na daný obsah databáze DATA aplikována}
4. LOOP: if NULL (RULES) then return FAIL; { není-li žádné další aplikovatelné pravidlo, končí procedura chybovým (fail) stavem a vrací symbol FAIL}
5. R FIRST (RULES); { aplikováno bude v pořadí první, resp. podle daného kritéria "nejlepší" pravidlo}
6. RULES TAIL (RULES); { z posloupnosti aplikovatelných produkčních pravidel je vyjmuto zvolené pravidlo}
7. NEW_DATA R (DATA); { na obsah databáze DATA je aplikováno produkční pravidlo R z posloupnosti RULES a je vygenerován nový obsah databáze NEW_DATA}
8. PATH BACKTRACK (NEW_DATA); { procedura BACKTRACK je vyvolána rekursivně pro nový obsah databáze}
9. if PATH = FAIL then goto LOOP; {vrátilo-li vyvolání procedury BACKTRACK chybový příznak FAIL, přechází na použití dalšího produkčního pravidla (pokud takové existuje)}
10. return CONS (R, PATH); { v opačném (úspěšném) případě je přidáno nově aplikované produkční pravidlo na čelo seznamu (vrchol zásobníku) reprezentujícího vygenerovanou cestu ve stromu řešení z počátečního uzlu do uzlu aktuálního}

Jak vyplývá z uvedeného algoritmu, mechanismus navracení nemusí vybírat produkční pravidla v každém kroku náhodně nebo podle zadaného pořadí, nýbrž pro výběr následujícího aplikovaného pravidla lze využít nějaké heuristiky. Na rozdíl od dokonalejších metod hledání v grafu (viz dále) je však použití heuristiky u backtrackingu vždy čistě lokální záležitostí, čili vždy je omezeno na jeden konkrétní uzel stromu řešení (pro každý uzel musí být definována speciální heuristika), což komplikuje formulaci algoritmu.

Příklad 2.3:

Několik prvních kroků postupu hledání řešení úlohy hlavolamu "8" v situaci, která byla uvedena na obr. 2.2, pomocí mechanismu navracení je uvedeno na obr. 2.3; celý strom řešení pak na obr. 2.4.

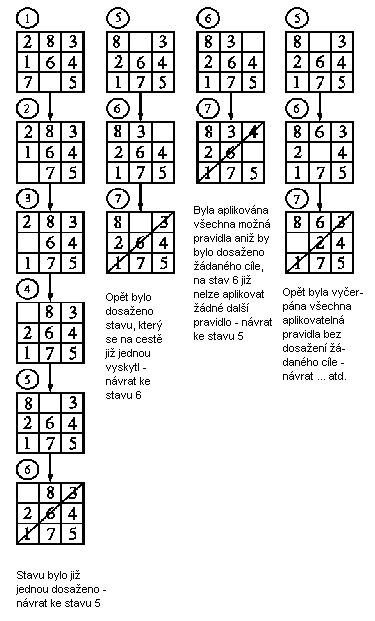
Obr. 2.3: Začátek postupu hledání řešení hlavolamu pomocí mechanismu navracení

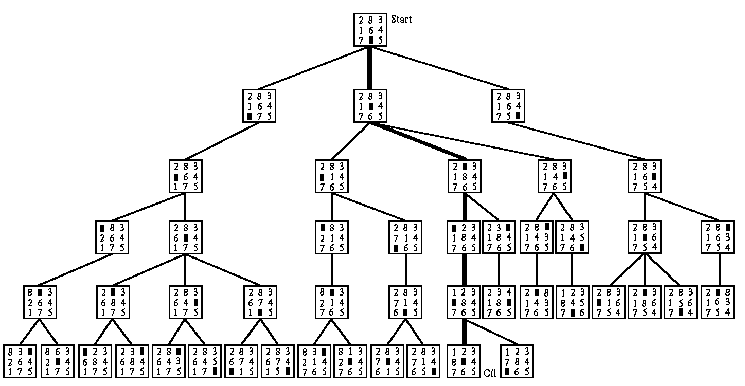
Obr. 2.4: Strom řešení úlohy hlavolam "8" při použití algoritmu navracení (tučně je vyznačena cesta nalezeného řešení)

Výše popsaný algoritmus mechanismu navracení se nazývá backtracking stavový, neboť kromě aplikovaných pravidel si "pamatuje" i stavy, resp. jim příslušné obsahy databáze (state-saving system). Kromě něj existuje ještě backtracking operátorový neboli Floydův. Ten v seznamu (zásobníku) reprezentujícím cestu od počátečního uzlu stromu řešení k uzlu aktuálnímu uchovává pouze aplikovaná produkční pravidla, což má výhodu v minimálních nárocích na obsazenou paměť. Na druhé straně je však Floydův algoritmus výrazně náročnější na čas výpočtu, protože při obnově obsahu databáze příslušejícího některému z předchozích stavů se musí znovu postupně vygenerovat všechny obsahy databáze od stavu počátečního až po stav hledaný. Vyšší časová složitost Floydova algoritmu pak je důvodem, proč se v převážné většině případů implementuje backtracking stavový.

2.5.2 Metody hledání v grafu

2.5.2.1 Základní algoritmus

Mechanismus navracení"zapomíná" všechny cesty ve stromu řešení, které skončily chybovým (fail) stavem. Pamatuje si pouze cestu od kořene k poslednímu vygenerovanému uzlu. Dokonalejší metody hledání v grafu (graph search) si naopak pamatují celou dosud vygenerovanou část stromu řešení. To má tu výhodu, že se zamezí zbytečnému opětovnému generování uzlů, s nimiž se řídicí mechanismus již setkal, ale na druhé straně má značné nároky na paměť (které ale dnes už nejsou problémem). Vhodně definovanými heuristikami se však dá generování stromu řešení poměrně hodně zredukovat. Díky tomu, že všechny vygenerované uzly jsou "zapamatovány", lze pro časově únosné nalezení řešení (cílového stavu) použít účinné globální heuristiky.

Pro hledání v grafu je typické, že na uzel stromu řešení (stav), resp. jemu odpovídající obsah databáze, aplikujeme všechna aplikovatelná produkční pravidla, čímž dostaneme všechny jeho bezprostřední následníky. Proces vygenerování všech možných bezprostředních následníků uzlu budeme v dalším nazývat expanzí uzlu}.

Dále budeme předpokládat, že máme k dispozici nějakou ohodnocující funkci, která pro každý obsah databáze (stav) vypočítá jeho kvantitativní ohodnocení.

Základní algoritmus hledání v grafu si pro jednoduchost znázorníme vývojovým diagramem uvedeným na obr. 2.5. Implementace algoritmu je založena na použití dvou seznamových struktur OPEN a CLOSED přičemž v seznamu OPEN jsou uloženy uzly, které dosud nebyly expandovány, a v seznamu CLOSED uzly, které již expandovány byly anebo se pro expanzi z nějakého důvodu nehodí.

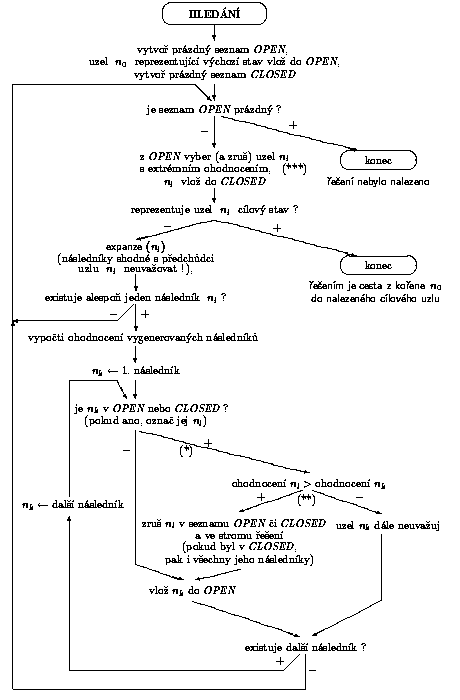
Obr. 2.5: Vývojový diagram základního algoritmu hledání v grafu

Abychom si blíže vysvětlili funkci základního algoritmu hledání v grafu, uvažujme hypotetický příklad podle obr.2.6. V kroku (***) algoritmu (viz obr.2.5) budeme brát v úvahu minimum ohodnocující funkce. Obr. 2.6 a zobrazuje strom řešení bezprostředně před expanzí uzlu n₂, který má v tomto okamžiku nejmenší ohodnocení (14). Nechť bezprostředními následníky uzlu n₂ jsou uzly n₄(14), n₇(14) a n₈(12), kde čísla v závorce udávají ohodnocení uzlů. Tyto uzly se již ve stromu řešení vyskytují, a proto budeme postupovat větví základního algoritmu označenou (*) .

Nově vygenerovaný uzel n₄(14) má vyšší ohodnocení než již existující uzel n₄(13), proto zrušíme nově vygenerovaný uzel n₄(14). Nově vygenerovaný uzel n₇(14) má nižší ohodnocení než existující uzel n₇(15), který je v seznamu OPEN, proto se podle (**) v obr. 2.5 zruší "starý" uzel. Nově vygenerovaný uzel n₈(12) má rovněž nižší ohodnocení než uzel n₈(13), který se nalézá v seznamu CLOSED. Podle (**) proto zrušíme "starý" uzel n₈(13) včetně všech jeho následníků n₉, n₁₁, n₁₂ ze seznamu OPEN a n₁₀ ze seznamu CLOSED. Situaci po expanzi uzlu n₂ ukazuje obr.2.6 b.

Základní algoritmus hledání v grafu má řadu variant. Výše uvedený postup hledání představuje jednoduchou a snadno implementovatelnou verzi. Tento algoritmus lze dále modifikovat v tom směru, že algoritmus neexpanduje uzel najednou, ale postupně generuje jednotlivé jeho bezprostřední následníky; expandovaný uzel je přesunut do seznamu CLOSED teprve tehdy, až jsou vygenerováni všichni jeho bezprostřední následníci. Taková modifikace je paměťově úspornější a obvykle rychlejší než výše uvedená základní verze.

Z implementačního hlediska je třeba poznamenat, že generovaný strom řešení se neuchovává v paměti jako zvláštní komplikovaná grafová struktura, nýbrž se využívá toho, že každý uzel (kromě kořene) má právě jen jednoho bezprostředního předchůdce. Ke každému uzlu v seznamu OPEN či CLOSED se proto kromě jeho ohodnocení přidává zpětný ukazatel na jeho bezprostředního předchůdce (obdoba binárních vyhledávacích stromů se zpětným zřetězením na bezprostředního (symetrického) předchůdce nebo následníka).

Výše zmíněná implementace vnitřně reprezentuje strom řešení úlohy, v němž pak snadno nalezneme hledanou výslednou cestu z počátečního do cílového stavu úlohy - hledané řešení. Od dosaženého cílového stavu budeme postupovat ve smyslu zpětných ukazatelů až k uzlu počátečnímu a vhodným způsobem nalezenou cestu uložíme. Udržování zpětných ukazatelů je poměrně jednoduché, a proto jsme ho v popisu základního algoritmu explicitně neuváděli.

2.5.2.2 Slepé strategie hledání řešení

Podle toho, zda pro prohledávání stromového grafu reprezentujícího graf řešení úlohy máme či nemáme k dispozici nějakou vhodnou heuristiku, rozlišujeme prohledávací strategie na slepé a cílené , resp. heuristické . V tomto odstavci objasníme případ, kdy žádnou vhodnou heuristiku k dispozici nemáme.

V úlohách umělé inteligence rozlišujeme dva typy strategie slepého hledání v grafu: strategii hledání do hloubky a hledání do šířky .

Strategie hledání v grafu do hloubky (depth--first search) dává při expanzi přednost těm uzlům, které mají největší hloubku. Hledání v grafu do hloubky představuje speciální případ základního algoritmu (obr. 2.5) takový, pro nějž platí:

• ohodnocení uzlu je rovno hloubce uzlu,
• v kroku (***) algoritmu se bere maximum ohodnocení,
• v kroku (***) ještě musíme přidat test, zda již bylo dosaženo zadané maximální hloubky prohledávání; pokud ano, pak se algoritmus vrací ke kroku předchozímu (tj. k testu, zda seznam OPEN je prázdný).

Maximální hloubka prohledávání musí být zadána z toho důvodu, že právě rozvíjená cesta nemusí vést k žádanému cíli, mohla by být nekonečně dlouhá a vyčerpali bychom přidělenou oblast paměti bez nalezení řešení, i když toto by mělo hloubku např. jen 2, ale leželo by na jiné cestě.

Použití strategie hledání do hloubky pro nalezení řešení hry "osmička" je ilustrováno obrázkem 2.7. Číselné údaje uvedené u jednotlivých uzlů grafu označují pořadí expanze uzlů, zadaná maximální hloubka generovaného stromu řešení byla rovna 5.

Poznámka 2.1: Hledání v grafu do hloubky a mechanismus navracení (backtracking) jsou velmi podobné algoritmy a liší se pouze v tom, že:

• při hledání do hloubky se generují najednou všichni bezprostřední následníci (je provedena expanze uzlu), zatímco podle algoritmu mechanismu navracení je generován pouze jediný následník (aplikací příslušného produkčního pravidla ve stanoveném pořadí) - viz odstavec 2.5.1.
• řídicí mechanismus si při hledání do hloubky "pamatuje" celý vygenerovaný strom řešení, zatímco mechanismus navracení pouze poslední větev.

Z těch důvodů se obvykle dává přednost mechanismu navracení, neboť je snáze implementovatelný a má výrazně nižší paměťovou složitost (nároky na paměť), pochopitelně za cenu vyšší algoritmické složitosti (časově delší výpočet).

Strategie hledání v grafu do šířky (breadth-first search) dává při expanzi přednost uzlům s nejmenší hloubkou. Jde opět o zvláštní případ základního algoritmu hledání v grafu s tím, že:

• ohodnocení uzlu je rovno hloubce uzlu,
• v kroku (***) algoritmu se bere minimum ohodnocení.

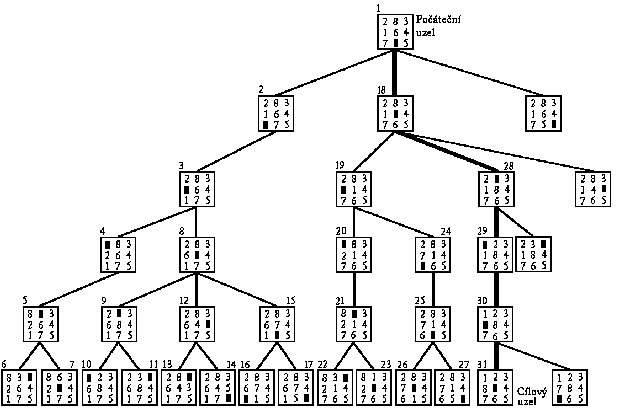
Obr. 2.7: Graf stromu řešení při hledání do hloubky

Příklad aplikace strategie hledání do šířky pro nalezení řešení hlavolamu "osmička" je uveden na obr. 2.8. Číselné údaje uvedené u jednotlivých uzlů grafu opět označují pořadí expanze uzlů. Při podrobnější analýze postupu hledání řešení pomocí strategie hledání do šířky zjistíme, že algoritmus vždy nalezne nejkratší cestu k cílovému uzlu (stavu), tj. "nejrychlejší" řešení, pokud ovšem takové řešení (taková cesta) vůbec existuje.

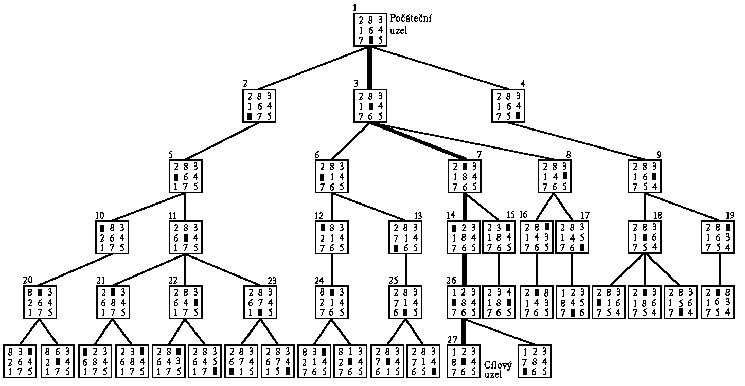
Obr.2.8: Graf stromu řešení při hledání do šířky

2.5.2.3 Heuristické strategie hledání řešení

Metody slepého hledání v grafu jsou obecně schopny najít cílový uzel, když povolíme dostatečnou hloubku stromu řešení. Je to však za cenu obrovského množství vygenerovaných uzlů stromu. Proto se obvykle při návrhu produkčních systémů snažíme nalézt nějakou heuristiku, která by nám pomohla nalézt řešení I při relativně malém počtu vygenerovaných uzlů. Takovým řídicím mechanismům se říká heuristické strategie hledání řešení.

Abychom mohli použít heuristiku u metod hledání v grafu, je třeba ji definovat např. v podobě ohodnocující funkce, která pro každý uzel (obsah databáze) poskytne kvantitativní ohodnocení. Heuristické metody hledání se pak řídí základním algoritmem hledání v grafu (obr.2.5) s tím, že v kroku (***) se uvažuje minimum} ohodnocující funkce. Pomocí ohodnocující funkce se ze seznamu OPEN vybírají pro expanzi "nejnadějnější" uzly. Nejčastěji se za ohodnocující funkci bere funkce, která určuje či odhaduje "vzdálenost" nebo "nákladnost" cesty mezi daným (právě ohodnocovaným) a cílovým uzlem grafu (či množinou cílových uzlů, existuje-li jich více). V různých hříčkách a hlavolamech můžeme za ohodnocení uzlu (obsahu databáze) vzít např. počet dosažených bodů, počet kostek (kamenů), které neleží na cílové pozici atp.

Jako příklad si ukažme činnost algoritmu heuristického hledání v grafu pro hlavolam "8". Uvažujme ohodnocující funkci ve tvaru

,

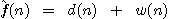kde
d(n) je délka cesty od počátečního uzlu k n-tému uzlu,
w(n) je počet kamenů v databázi n-tého uzlu neležících na svých místech.

Strom řešení hlavolamu "8" pomocí výše uvedené heuristické funkce je uveden na obr.2.9 na následující stránce. Čísla nad levým horním rohem struktury reprezentující stav (uzel grafu) udávají pořadí, v němž byly uzly expandovány, čísla v kroužcích pak ohodnocení uzlu (stavu databáze) při použití výše definované heuristické funkce.

Poznámka 2.2: Za povšimnutí stojí fakt, že pokud bychom ohodnocující (heuristickou) funkci definovali jako 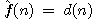, dostali bychom metodu hledání do šířky.

Při heuristickém hledání v grafu se obvykle požaduje, aby byla nalezena optimální cesta od počátečního do cílového uzlu, tj. např. cesta s minimální cenou. Kromě toho se též požaduje, aby náklady na hledání (tj. doba výpočtu a počet vygenerovaných uzlů grafu) byly co nejmenší. Tyto požadavky jsou však protichůdné: požadujeme-li nalezení optimální cesty, musíme vygenerovat mnoho "nadějných" uzlů; nebudeme-li naopak generovat všechny "nadějné" uzly, může se stát, že nalezená cesta nebude optimální.

V následujícím odstavci si ukážeme, jaké podmínky musí splňovat ohodnocující funkce, aby zajišťovala nalezení optimální (nebo alespoň suboptimální) cesty, a za jakých podmínek lze snížit náklady na hledání řešení.

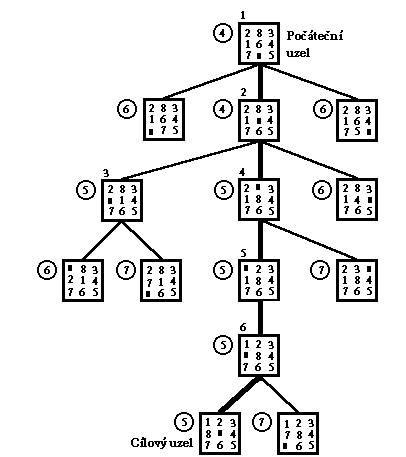
Obr.2.9: Graf stromu řešení při heuristickém hledání v grafu

2.5.2.4 Algoritmus A^*

Optimální cesta z počátečního do cílového uzlu je - jak již bylo řečeno - cesta s minimálními náklady (minimální cenou). Je proto vhodné definovat funkci f^*(n), která jako výsledek poskytuje skutečnou (minimální) cenu optimální cesty z výchozího uzlu grafu do uzlu cílového procházející uzlem n. Tuto cenu můžeme principiálně rozdělit na dvě složky

,

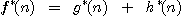kde
g^*(n) je cena optimální cesty z výchozího uzlu do uzlu n,
h^*(n) je cena optimální cesty z uzlu n do uzlu cílového.

Při hledání řešení úlohy však optimální cestu àpriori neznáme a neznáme proto ani tvar funkce 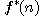. Nezbývá nám nic jiného, než funkci 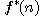odhadnout. Odhady heuristické funkce 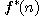označíme 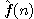, resp. 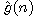a 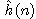. Potom platí

,

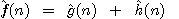kde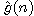
je odhad ceny optimální cesty z výchozího uzlu do uzlu n,
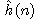je odhad ceny optimální cesty z uzlu n do uzlu cílového a
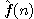je odhad ceny optimální cesty z výchozího uzlu do cílového vedoucí přes uzel n.

Jako funkci 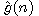lze vzít nejmenší dosud nalezenou cenu cesty z výchozího uzlu do uzlu n ve stromu řešení, který byl do daného okamžiku vygenerován. Tzn., že 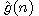dostaneme součtem cen všech hran na cestě z výchozího uzlu do uzlu n ve vygenerovaném stromu řešení. Zjevně platí, že 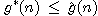, neboť stále může existovat dosud nevygenerovaná cesta se skutečně minimální cenou.

Stanovení funkce 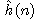je velmi obtížné. Můžeme spoléhat jen na heuristickou informaci, která je k dispozici pro řešenou úlohu. Proto se někdy funkce 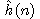nazývá ryze heuristickou} funkcí (pouze složka 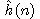funkce 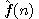je nositelem heuristické informace, hodnota funkce 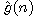je zpravidla určena deterministickým výpočtem). Příkladem odhadu 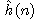je funkce w(n) z předchozího příkladu řešení hlavolamu "8".

Základní algoritmus hledání v grafu, který za ohodnocující funkci bere funkci definovanou jako 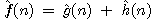, se nazývá algoritmus A. Jestliže však ryze heuristická funkce 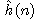je nezáporným dolním odhadem} funkce 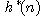, tj. pro každé n platí

,

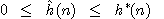dostáváme "optimální" verzi algoritmu A nazývanou jako algoritmus A* (čteme "A - star").

Poznámka 2.3:
Všimněme si, že při 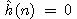a jednotkových cenách hran stromu řešení úlohy platí 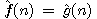a dostáváme tak algoritmus hledání do šířky. Navíc se jedná o algoritmus A*, neboť 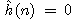je dolním odhadem (i když určitě ne nejlepším) pro každou funkci h^*(n).

Poznámka 2.4:
Říkáme, že algoritmus prohledávání stromu řešení je přípustný, jestliže skončí svoji činnost nalezením optimální cesty (tj. cesty s např. optimální cenou) z výchozího do cílového uzlu v libovolném grafu, pokud tato cesta existuje. Dá se dokázat [Nilsson82], že algoritmus A* je přípustný.

Poznámka 2.5:
Na heuristickou funkci algoritmu A* mohou být kladena některá další omezení. Nejčastěji se požaduje její monotónnost. Omezující podmínka pro definici monotónní heuristické funkce připomíná trojúhelníkovou nerovnost [Nilsson82]. Její podrobnější rozbor přesahuje rámec tohoto skripta. Pomocí ní však můžeme dokázat, že jakmile se algoritmus A* s monotónní heuristickou funkcí rozhodne expandovat nějaký uzel n, potom cesta vedoucí z výchozího uzlu do uzlu n je již optimální, neboli 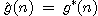. Z toho dál plyne, že hodnoty 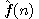posloupnosti expandovaných uzlů jsou nerostoucí posloupností. Dalším důsledkem je, že u uzlu vybraného pro expanzi není třeba kontrolovat, zda se vyskytuje v seznamu CLOSED, čili seznam CLOSED při realizaci metody nemusíme vůbec zavádět. Jinými slovy, "navádění" na cílový uzel grafu řešení úlohy pomocí monotónní heuristické funkce je natolik přesné, že nehrozí nebezpečí zacyklení a vzhledem k nízkému počtu vygenerovaných, resp. expandovaných uzlů se výrazně snižují nároky na čas potřebný pro porovnávání aktuálních obsahů databáze. Na závěr ještě poznamenejme, že ryze heuristická funkce 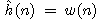a samozřejmě pak také 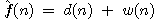z předchozího příkladu hlavolamu "8" jsou funkce monotónní.

2.5.2.5 Efektivnost algoritmů hledání v grafu

Kdybychom při hledání řešení úlohy požadovali jen nalezení optimální, např. nejkratší cesty od výchozího k cílovému uzlu, vystačili bychom s algoritmem hledání do šířky. Ten však, jak víme, nemá žádnou "heuristickou sílu", což se jako negativní důsledek projeví v enormně vysokém počtu generovaných uzlů grafu. My však z hlediska efektivnosti algoritmu zpravidla požadujeme, aby počet generovaných uzlů stromu řešení nebyl příliš vysoký, čili vygenerovaný strom řešení nebyl příliš "košatý".

Dá se dokázat [Nilsson82], že více informovaný algoritmus typu A^* při své činnosti vygeneruje méně uzlů stromu. Přitom více informovaným} algoritmem rozumíme algoritmus s funkcí 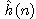, která je těsnějším (lepším) dolním odhadem funkce h^*(n). Více informovaný algoritmus tak vyžaduje přesnější heuristickou informaci. Na druhé straně však generování méně košatého stromu řešení neznamená, že algoritmus je efektivnější. Více informovaný algoritmus se složitějším algoritmem výpočtu heuristické funkce může spotřebovat více času právě na výpočet ohodnocení uzlů pomocí složitější heuristické funkce.

Vidíme, že efektivnost algoritmu hledání řešení závisí především na tvaru (algoritmické složitosti) heuristické funkce. Při jeho výběru, resp. jeho formulaci, nám nepomůže žádná teorie, musíme se spoléhat jen na adekvátnost analýzy úlohy či na vlastní intuici.

Na závěr si proto zopakujme, že efektivnost algoritmu hledání řešení určují následující faktory:

• cena cesty od výchozího do cílového uzlu stromu řešení úlohy,
• počet vygenerovaných uzlů ("košatost") stromu řešení,
• algoritmická složitost výpočtu heuristické funkce.

Efektivnost algoritmu hledání řešení lze v některých případech zlepšit tím, že nebudeme požadovat, aby funkce 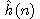byla dolním odhadem funkce h^*(n). Tak lze řešit i poměrně komplikované úlohy, avšak za cenu, že nalezené řešení nemusí být optimální, a pochopitelně při realizaci metody musíme použít seznam CLOSED (viz výše uvedená poznámka č.3).

Jako příklad uveďme opět úlohu hlavolamu "8" s cílovým stavem definovaným stejně jako v odstavci 2.2  (obr.2.1). Ryze heuristickou funkci 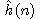definujeme pomocí vztahu

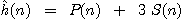
kde P(n) je součet vzdáleností každého kamene od svého cílového místa (v počtu možných posunů kamenů) a S(n) je míra porušení pořadí kamenů: za každý kámen nenacházející se ve středu hracího pole, který není následován správným kamenem (ve smyslu definovaného cílového stavu řešení úlohy), přičítáme dvě, za kámen ve středu pole přičítáme hodnotu 1.

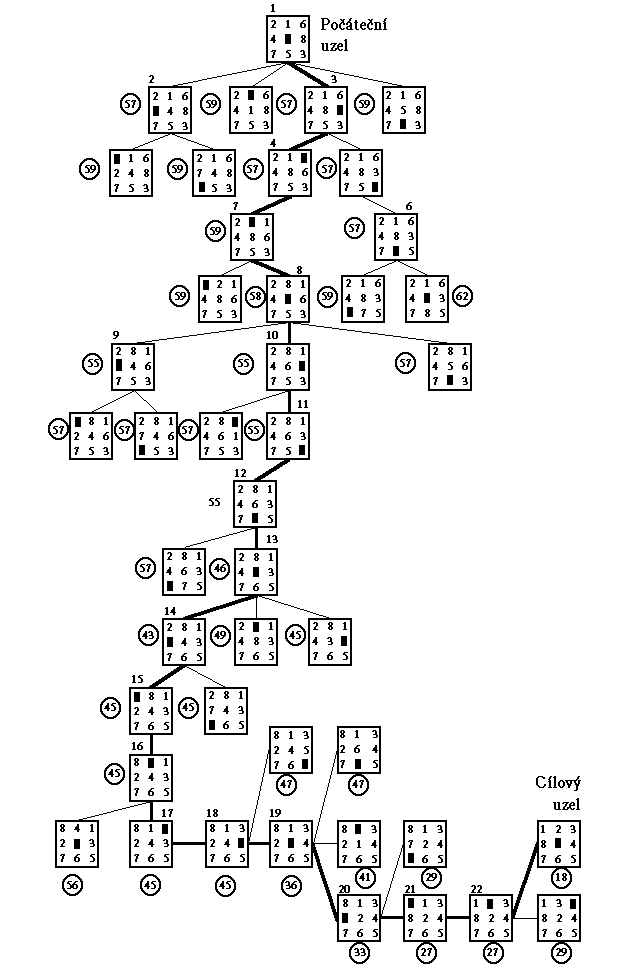
Obr. 2.10: Strom řešení "8" při použití funkce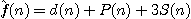

Není snad třeba zdůrazňovat, že výše uvedená definice složky ryze heuristické funkce S(n) platí pouze pro případ cílové konfigurace hlavolamu "8" definované v odst. 2.2, tj. s prázdným místem uprostřed hracího pole; pro jinou cílovou konfiguraci hlavolamu bychom funkci S(n) museli definovat analogicky, tj. např. při cílovém stavu 1-2-3; 4-5-6; 7-8-0 (zapsáno "po řádcích") za kámen v pravém dolním rohu hracího pole přičítat 1 atd.

Výše uvedeným způsobem definovaná funkce 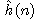však není dolním odhadem funkce h^*(n). Přesto při jejím použití algoritmus hledání řešení postupuje poměrně rychle k hledanému cílovému stavu (viz obr.2.10). Ačkoli nejde o algoritmus A* a není zaručeno nalezení optimální cesty, byla v uvedeném příkladě optimální cesta pomocí výše definované heuristické funkce nalezena.

Díky nedeterminismu při řešení úloh (viz odstavec 2.2) známe v současnosti jedinou obecnou metodu řešení induktivních úloh, u nichž není k dispozici heuristická informace - slepé prohledávání grafu řešení úlohy, při němž explicitně sestrojujeme strom řešení úlohy, který vylučuje "zabloudění" do nekonečného cyklu (viz odstavec 2.4). Protože velikost stromu řešení obecně exponenciálně narůstá s jeho hloubkou, je tato metoda mimořádně náročná na čas výpočtu a obsazení paměti počítače. Z toho důvodu je účelné používat heuristiky, které více či méně "ořežou" větve stromu řešení na přijatelnou míru a tím usnadní dosažení cílového stavu.

Metoda heuristického hledání v grafu popsaná v předchozím odstavci dovoluje využít jen takové heuristiky, ze kterých dokážeme sestavit nějakou ohodnocující funkci. Pro řadu úloh je ovšem obtížné či dokonce nemožné takové heuristiky zformulovat. Někdy však lze získat heuristiky jiného druhu, kterými lze původní úlohu rozložit na konečný počet dílčích úloh (podúloh), které jsou snáze řešitelné. Pokud podúloha není elementární úlohou, tj. takovou, že ji lze ve smyslu produkčního systému realizovat aplikací jediného produkčního pravidla, můžeme se pokusit znovu ji rozložit na další dílčí úlohy (podúlohy) atd.

Rozklad úlohy na podúlohy si můžeme ukázat na jednoduchém příkladě klasické úlohy přemisťování hanojských věží. V počátečním stavu úlohy je hanojská věž skládající se z N kotoučů o různých průměrech situována na levém kolíku, který označme A (viz obr. 2.11). úkolem úlohy je přemístit jednotlivé kotouče na pravý kolík (označený C) s pomocí středního kolíku B tak, že se smí vždy přemisťovat jen vrchní kotouč a žádný kotouč nesmí nikdy ležet na kotouči menšího průměru. Kotouče označme podle velikosti (průměru) celými čísly 1, 2, ..., N.

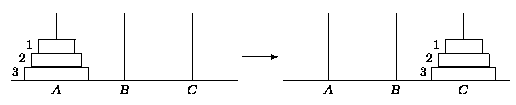
Obr. 2.11:  úloha "Hanojské věže"

Libovolný stav úlohy popíšeme seznamem [A, B, C], kde symboly A, B, C představují seznamovou reprezentaci uložení kotoučů na kolíku A, B, resp. C v pořadí shora dolů. Nenachází-li se na kolíku žádný kotouč, bude seznam prázdný (reprezentace pomocí nil). Na obr. 2.11 vyobrazená úloha se pak dá symbolicky zapsat jako

.

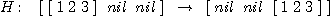Takto definovanou úlohu můžeme rozložit na tři dílčí úlohy, které budou představovat převedení výchozího stavu úlohy přes dva mezistavy do cílového stavu. Pomocí výše uvedené seznamové symboliky lze rozklad na podúlohy zapsat následovně:

, , .

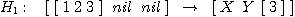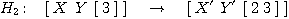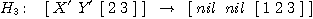Podíváme-li se blíže na podúlohu H₃, je zřejmé, že pomocné proměnné X' a Y' označují situaci [1] nil, resp. nil [1], protože kotouč 1 musí ležet buď na kolíku A nebo B. Obdobně pomocné proměnné X a Y v dílčí úloze H₂ symbolicky reprezentují situaci [1 2] nil, [1][2], [2][1], resp. nil [1 2]. Rovněž můžeme snadno ukázat, že takové řešení je optimální, protože použití tohoto rozkladu úlohy na podúlohy vyžaduje generování právě 2^N-1 uzlů (zde 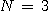), což je délka nejkratšího řešení.

2.6.1 AND/OR grafy

Rozklad úlohy na podúlohy se obvykle znázorňuje grafem, jehož uzly reprezentují úlohu či jednotlivé podúlohy a uzly, které nejsou listy, jsou dvojího typu (viz obr. 2.12):

• AND - uzly představují konjunkci podúloh, tj. k řešení úlohy (podúlohy) reprezentované AND - uzlem je nutné, aby byly řešeny všechny dílčí úlohy (tzn. všechny dílčí úlohy musejí být řešitelné); AND - uzly jsou zobrazovány v grafu tak, že hrany vycházející z tohoto uzlu jsou spojeny obloučkem;
• OR - uzly představují disjunkci podúloh; k řešení úlohy (podúlohy) reprezentované OR - uzlem postačí, aby byla řešena alespoň jedna z podúloh (alespoň jedna z podúloh musí být řešitelná).

Takto definovaný graf rozkladu úlohy na podúlohy se nazývá AND/OR grafem a někdy bývá též nazýván transformačním nebo konjunktivně disjunktivním grafem [Havel80]. Rozklad symbolické úlohy G na podúlohy G₁ až G₇ znázorněný pomocí AND/OR grafu je zobrazen na obr. 2.12, rozklad úlohy přemisťování kotoučů mezi kolíky Hanojských věží na dílčí podúlohy můžeme pak symbolicky vyjádřit AND/OR grafem zobrazeným na obr. 2.13. Elementární podúlohy jsou na uvedených obrázcích vyznačeny dvojitým rámečkem.

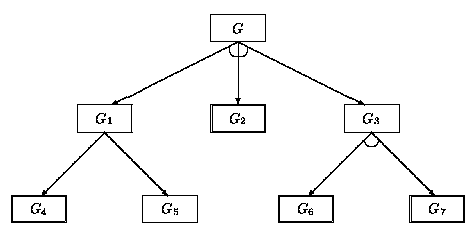
Obr. 2.12: AND/OR graf rozkladu symbolické úlohy G

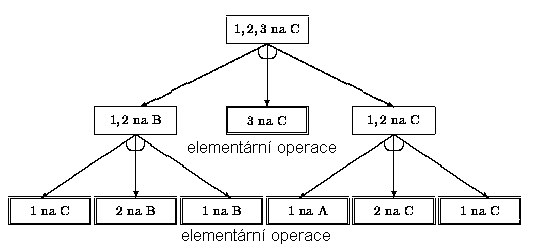
Obr. 2.13: AND/OR graf rozkladu úlohy "Hanojské věže"

Symbolické integrování je jedna z metod umožňujících rozklad úlohy na podúlohy. Operátory, které redukují danou úlohu na podúlohy, mohou být založeny na pravidlu integrování per-partes, na výpočtu integrálu součtu (součtu integrálů), vytýkání konstanty před integrál a různých typech substitucí. Jeden příklad možného rozkladu problému řešení neurčitého integrálu na podproblémy je uveden na obr. 2.14 (obrázek byl převzat z [Nilsson82]).

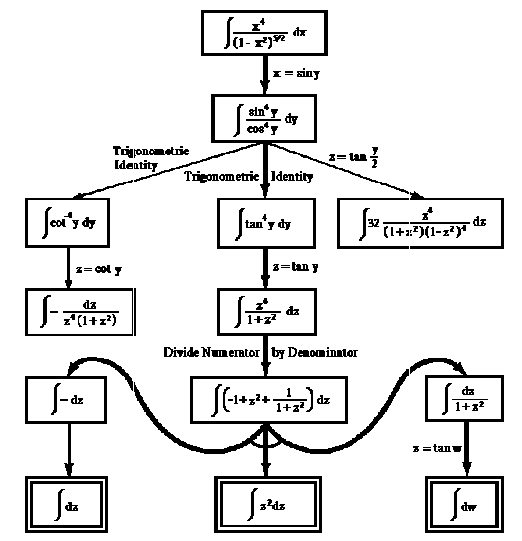
Obr. 2.14: AND/OR graf rozkladu úlohy řešení neurčitého integrálu

V tomto odstavci se jen velmi stručně zmíníme o některých programových systémech, resp. programových balících, které byly v minulých létech pro řešení jednodušších úloh ve světě vyvinuty a významně přispěly k rozvoji umělé inteligence.

2.7.1 Programový systém GPS

GPS je zkratka pro General Problem Solver  (obecný řešitel úloh). Jeho první návrh vznikl na konci padesátých let a byl inspirován tehdejšími poznatky z psychologie lidského myšlení. Řadou autorů byl rozvíjen až do počátku sedmdesátých let a při jeho vývoji šlo mj. o dosažení následujících dvou cílů:

1. ukázat, jak lze počítače využít pro řešení úloh vyžadujících inteligenci,
2. přispět k poznání, jak člověk takovéto úlohy řeší (cíl pro umělou inteligenci poněkud netypický).

Teoretickým přínosem systému GPS je metoda nazvaná analýza prostředků a cílů. Princip metody je založen na postupném rozkladu úloh na podúlohy metodou výpočtu diferencí [Kotek86]. GPS vychází z diferencí mezi počátečním a cílovým stavem řešení úlohy a snaží se tyto diference postupně zmenšovat. Jednotlivé diference uspořádává podle důležitosti pro řešení, různým druhům diferencí je přiřazen různý význam a snahou systému je zmenšovat vždy nejvýznamnější diferenci.

GPS se při své činnosti může dostat do stavu, ve kterém se již nacházel. Aby se nedostal do nekonečného cyklu, musí si vést seznam již vygenerovaných stavů, který je analogický k seznamu CLOSED u obecného algoritmu hledání v grafu. Pomocí tohoto seznamu, který je implementován jako zásobník, GPS v případě potřeby uskuteční návrat k předchozímu stavu. Kromě tohoto seznamu (zásobníku) GPS používá další zásobník pojmenovaný OBJECTS.

Činnost GPS můžeme popsat následovně: Cílový stav poslední vyřešené podúlohy se nachází na vrcholu zásobníku OBJECTS. Poslední vyřešená úloha měla za úkol odstranit určitou diferenci, která v daném okamžiku byla nejdůležitější. Vlivem vedlejších efektů se však mohlo stát, že se obnovila některá z ještě závažnějších diferencí, která byla již jednou odstraněna. Tato diference je v daném okamžiku nejdůležitější a proto zvláštní procedura sestaví korekční podúlohu, která má tuto obnovenou diferenci znovu odstranit.

Vlastní řešení podúlohy začíná procedurou, která se snaží vybrat produkční pravidlo, které by danou diferenci odstranilo nebo ji co nejvíce zmenšilo. Poté se GPS snaží vybrané pravidlo na daný stav úlohy aplikovat. Nejde-li to, určí proč a tuto informaci předá zpět proceduře hledající produkční pravidlo. Tento postup rekurzivně opakuje tak dlouho, až je buď možné celou sekvenci hledaných pravidel aplikovat a tím odstranit diference, nebo skončí neúspěchem, není-li podúloha řešitelná. Podrobnější popis systému GPS je uveden v [Havel80].

2.7.2 Programový systém STRIPS

STRIPS je programový systém, který byl vyvíjen od počátku sedmdesátých let jako následovník systému GPS a pochopitelně využívá všech poznatků získaných při vývoji GPS. Vývoj STRIPSu byl motivován aplikací v oblasti navrhování a konstrukce inteligentních robotů, avšak jeho základní algoritmus má obecné využití.

Stavy řešené úlohy jsou popsány formulemi predikátového počtu 1.řádu v klausulárním tvaru (viz následující kapitola skripta), je specifikován počáteční a cílový stav úlohy. Pravidla pro přechody mezi stavy jsou popsána trojicemi (C,D,A), kde C je podmínka aplikovatelnosti pravidla, D je množina klausulí, které budou z popisu stavu vynechány, použije-li se toto pravidlo, a A je množina klausulí, které budou v případě aplikace pravidla přidány. V procedurální sémantice nehovoříme o odstraňování diferencí, ale o splňování cílů. Principiálně to znamená, že objeví-li se nová diference, vznikl nový cíl, který je třeba splnit.

Řešení úlohy systémem STRIPS začíná tím, že se systém snaží splnit zadaný cíl řešení. Jestliže cíl koresponduje se specifikovaným cílovým stavem, je řešení úlohy úspěšně ukončeno, protože popis řešení byl zadán v počáteční databázi. Jestliže ne, snaží se systém vybrat takové produkční pravidlo, v jehož seznamu se vyskytl fakt korespondující se zadaným cílem. Najde-li takové pravidlo, musí stejným způsobem pokračovat v plnění cílů uvedených v samostatném seznamu cílů pravidla. Tento rekursivní proces skončí tehdy, když jsou všechny cíle splněny.

Uvedený postup je však jen pouhým náčrtem postupu STRIPSu. Náčrtem proto, že při jeho sestavování STRIPS neuvažoval vedlejší (postranní) efekty provedení pravidel. Tento "hrubý" náčrt postupu, který v dalším nazveme plánem}, nemusí být jednoduše realizovatelný a musí se "odladit". "Ladění" plánu provádí systém automaticky, a to tak, že postupně aplikuje produkční pravidla a jakmile zjistí nesrovnalost v aplikovatelnosti pravidla na aktuální stav databáze, stanoví si jako nejbližší cíl její odstranění. Splňování nově stanoveného cíle probíhá naprosto stejným postupem. STRIPS opět nejprve vytvoří náčrt plánu a potom postupně prověřuje jeho realizovatelnost (splnitelnost). Takovéto "etapy" se postupně vnořují do sebe do libovolné hloubky tak dlouho, až lze původní plán plně realizovat nebo se zjistí (dokáže), že zadaná úloha nemá řešení.

2.7.3 Programový systém PLANNER

Programový systém PLANNER byl vyvíjen v MIT (Massachusetts Institute of Technology) paralelně k systému STRIPS. Představoval však ve své době významný pokrok především proto, že jako první využíval procedurální reprezentace znalostí (viz čtvrtá kapitola tohoto skripta). PLANNER reprezentuje konkrétní i obecné poznatky pro řešení úlohy obdobně jako STRIPS. Rozdíl je však v tom, že nepřipouští, aby fakta spojená s konkrétní situací (popisující konkrétní situaci - stav v řešení) obsahovala proměnné. Striktně rozlišuje specifické poznatky o konkrétní řešené úloze a obecné poznatky vztahující se k dané úloze. Obecné poznatky platí všeobecně pro celou třídu úloh a proto mají ve své reprezentaci proměnné, za které se podle potřeby dosazují konkrétní objekty.

Specifické poznatky o konkrétních předmětech (objektech) se nazývají fakta a jsou uloženy v databázi. Jak už bylo řečeno, výrazy reprezentující konkrétní fakta nesmí obsahovat proměnné. Fakta jsou v systému PLANNER reprezentována deklarativně (využívají deklarativní reprezentaci znalostí - viz dále). Pomocí faktů nelze tudíž vyjádřit obecné poznatky. Ty se ukládají do báze znalostí v podobě pravidel}. Pravidla obsahují informaci, za jakých podmínek mohou být použita a jak jejich provedení ovlivní obsah databáze. Pravidla jsou tedy nositeli procedurální} reprezentace znalostí.

U pravidel systému PLANNER rozlišujeme hlavu pravidla a jeho tělo. Tělo obsahuje posloupnost příkazů realizujících operaci, hlava pravidla je jeho popisem (obdobně jako hlavička procedury) umožňujícím jeho vyvolání. Pravidlo může být aplikováno jen na ty výrazy, které korespondují s jeho hlavou. Užití funkce goal (cíl) v těle pravidla má v systému PLANNER zásadní význam, neboť definuje pravidla, která se snaží splnit cíl, jenž je jejich argumentem.

Jestliže bychom systém PLANNER chtěli stručně charakterizovat, pak se jedná o pravidlový dedukční systém, který pracuje jak v přímochodém, tak i ve zpětnochodém režimu (viz čtvrtá kapitola), přičemž při dedukci využívá převážně režimu zpětnochodého.

2.7.4 PROLOG

Programovací jazyk PROLOG je v současné době nejrozšířenějším programovým systémem používaným pro řešení úloh umělé inteligence. Určen je především pro řešení problémů, v nichž se vyskytují objekty různých typů a relace nad nimi. PROLOG převzal některé myšlenky a techniky ze systému PLANNER a jeho základní ideou je využití logického kalkulu (zde predikátového počtu) pro programování. Je základním představitelem jazyků pro logické programování a bude mu věnována pozornost v následující kapitole skripta.