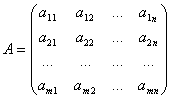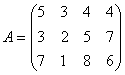Úvod do teorie her

Úvod

Předpokládáme, že o systému, v němž rozhodujeme vše podstatné víme, nebo můžeme předem zjistit a že systém nevykazuje vlastní aktivitu, kterou by mohl ovlivnit konečný efekt našich rozhodnutí.

Definice hry v normálním tvaru:

Dva hráči, označme je A a B, hrají hru podle těchto pravidel: je dána množina X s prvky x a množina Y s prvky y. x a y budou zpravidla čísla nebo funkce. Dále je dána omezená reálná funkce E(x,y), definována pro všechny dvojice (x,y), kde xX, yY. Hráč A volí z množiny X prvek x a hráč B volí z množiny Y prvek y, přičemž obě volby jsou na sobě nezávislé. Potom hráči své volby zveřejní a hráč B "zaplatí" hráči A částku E(x,y). Předpokládá se, že oba hráči znají X,Y a tvar funkce E(x,y).

Množinu X budeme nazývat prostorem strategií A a X prostorem strategií hráče B. Prvky jednotlivých strategií x, y nazveme pak strategiemi hráčů A a B. Funkci E(x,y) nazveme výplatní funkci. Nevylučujeme záporné hodnoty E(x,y), v tom případě hráč A zaplatí hráči B částku |E(x,y)|.

V souvislosti se hrami budeme dále vyšetřovat pouze tyto dva případy chování hráče B. 

• Hráč B je inteligentní a snaží se minimalizovat výplatní funkci, tj. částku E(x,y), kterou má zaplatit hráči A. V tom případě budeme mluvit o hře hrané podle minimaxu.

• Hráč B je lhostejný k výši částky E(x,y), kterou má zaplatit hráči A. V tom případě budeme mluvit o hře hrané proti přírodě.

V případě her hraných podle minimaxu mohou logicky nastat čtyři případy:

1. Je-li x' taková optimální strategie hráče A a y' optimální strategie hráče B, je rozumné požadovat, aby platilo E(x,y')<=E(x',y')<=E(x',y) pro všechny xX, yY. Levá nerovnost vztahu říká, že jestliže se hráč A  odchýlí od své optimální strategie, může na tom nejvýše prodělat, neboť jeho protivník je inteligentní a bude tedy volit svou optimální strategii y'. Pravá nerovnost podobně říká, že odchylka od optimální strategie u hráče B může znamenat nejvýš ztrátu pro něj. Vidíme také že je x',y' bodem, ve kterém funkce E(x,y) nabývá maxima pro xX a současně minima pro yY. Odtud název minimax. Číslo E(x,y) se nazývá cena hry.

2. Existuje optimální strategie x' hráče A a neexistuje optimální strategie hráče B. Míníme tím, že pro každou volbu strategie hráče B je pro A výhodná volba x', tj. E(x,y)<=E(x',y) pro všechna xX, yY, zatímco pro hráče B neexistuje strategie y', která by splňovala E(x',y')<=E(x',y) pro všechna yY.

3. Existuje optimální strategie hráče B a neexistuje optimální strategie hráče A.

4. Neexistuje optimální strategie pro žádného z hráčů.

Příklady her y bodů 2, 3 a 4.

X = <0,1>, Y = (0,1>, E(x,y) = x + y

X = <0,1), Y = <0,1>, E(x,y) = x + y

X = <0,1), Y = (0,1>, E(x,y) = x + y

 

Maticové hry

Definice maticové hry: 

Je dána matice čísel

Hráč A zvolí řádku, hráč B sloupec, potom oba své volby zveřejní a hráč B zaplatí hráči A tolik, kolik udává číslo na průsečíku řádky zvolné A a sloupce zvoleného B. Je-li číslo záporné, rozumíme tím, že A platí B jeho absolutní hodnotu.

Příklad

 

x' je optimální strategie hráče A a y' je optimální strategie hráče B. Prvek a₁₂=3 má totiž vlastnosti požadované ze vztahu (3). Cena hry je a₁₂=3.

 

Definice smíšeného rozšíření hry:

Budiž dána hra v normálním tvaru s prostory strategií X', Y', jejichž prvky jsou čísla, a s výplatní funkcí E'(x',y'). Smíšené rozšíření této hry je hra v normálním tvaru s prostory strategií X, Y a s výplatní funkcí E(x,y), kde za prostor X se bere nějaká množina pravděpodobnostních rozložení na X a za prostor Y nějaká množina pravděpodobnostních rozložení na Y a za výplatní funkci funkce

Integrál v posledním vztahu se chápe jako Lebesque-Stieltjesův a x(x') značí distribuční funkci rozložení x a podobně, y(y') distribuční funkci rozložení y.

Nekonečné hry

Při maticových hrách měl každý z hráčů konečný počet akcí, pro které se mohl rozhodnout. Hráč A mohl volit jeden z konečného počtu řádků, hráč B jeden z konečného počtu sloupců.

Mnohé rozhodovací situace však vyžadují provést jednu akci z nekonečna mnoha možných - nekonečné hry.

Zatímco každou maticovou hru lze řešit pomocí lineárního programování, u nekonečných her neexistuje žádná univerzální metoda řešení. Situace je podobná jako při řešení diferenciálních rovnic, pro každý typ her je nutné použít jiný způsob řešení, pokud ovšem vůbec nějaký způsob znám je.

Některé z her lze popsat pomocí bodů konečně-rozměrných euklidovských prostorů.

Hry proti přírodě

Hlavní otázka je, jak optimálně rozhodovat v situacích, které lze sice modelovat hrou v normálním tvaru, ale kde není rozumné předpokládat, že by hráč jednal tak, aby záměrně snížil hodnotu funkce E(x,y). to odpovídá situacím, kde protějškem hráče A je příroda nebo instituce, které je počínání hráče A lhostejné. Pro rozhodování se nejčastěji používá Bayesův princip:

Nechť X, Y jsou prostory strategií, E(x,y) je výplatní funkce. Známe-li jakou strategii y'Y bude proti hráči A příroda používat, je optimální strategií hráče A ta strategie x'X, pro kterou je  

 

 

maximální. Ve výrazu značí y'(y') distribuční funkci strategie y'.  

Je možné hru dvou osob rozšířit na hru n osob a to buď s nulovým součtem nebo hru n osob s nenulovým součtem.

Podrobněji v [9].